Bonjour ! Aujourd'hui nous allons voir quelque chose d'un peu plus théorique que d'habitude : la complexité algorithmique.
Je me permets de faire un aparté : n'étant pas un spécialiste de la complexité algorithmique, je ne rentrerai pas dans les détails des opérations mathématiques.
La complexité algorithmique est un moyen mathématique de déterminer la performance d'un algorithme en fonction de la taille et de la nature des données.
Pour mesurer cette performance, nous avons besoin d'évaluer le nombre d'opérations élémentaires (affectation, comparaison...) qui sont effectuées dans l'algorithme étudié.
Il existe quelques configurations caractéristiques pour évaluer un algorithme :
- Le meilleur cas ;
- Le pire des cas ;
- Le cas moyen.
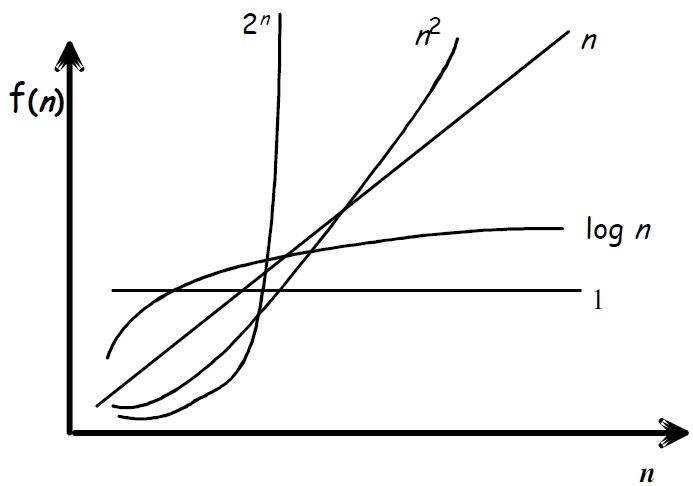
La notation " big oh " est la plus courante. Voici la plupart des notations, par ordre de performance :
- O(1) : temps constant (très bon)
- O(logn) : logarithmique (bon)
- O(n) : linéaire (bon dans certains cas)
- O(n×logn) : tris (par échanges)
- O(n²) : quadratique, polynomial (mauvais)
- O(2n) : exponentiel (problèmes très difficiles)
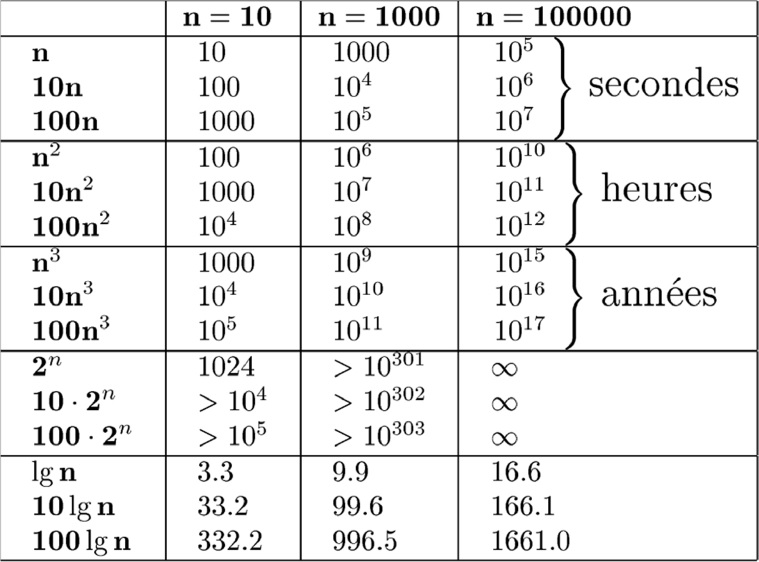
Ce tableau représente le temps que mettrais un algorithme en O(...) à s'exécuter en fonction de n élément.
Une représentation un peu plus graphique:
Je vous propose de regarder ensemble quelques petits exemples pour illustrer tout ça:
DÉBUT n <- 100 POUR compteur <- 0 JUSQU'À n FAIRE ECRIRE compteur FINPOURFINLa complexité de cet algorithme est en O(n) car il faut n instructions pour arriver à la fin de l'algorithme.
DÉBUT n <- 100 POUR i <- 0 JUSQU'À n FAIRE POUR j <- 0 JUSQU'À n FAIRE ECRIRE "i:", i,"j:",j FINPOUR FINPOURFINVoici une complexité de O(n²), de manière générale, les boucles imbriquées sont en O(n²).
DÉBUT n <- 100 POUR i <- 0 JUSQU'À 10000 FAIRE ECRIRE "i:", i FINPOURFINVoici une complexité de O(1), en effet peu importe la taille des données, le nombre d'opérations élémentaires reste constant.
DÉBUT n <- 20 POUR i <- 0 JUSQU'À n FAIRE POUR j <- 0 JUSQU'À (n * n) FAIRE ECRIRE "i:",i, "j:",j FINPOUR FINPOURFINCet algorithme est en O(n^3). Regardez bien la condition d'arrêt de la boucle *POUR *imbriquée: il faut effectuer n² opérations pour satisfaire la condition.
Pour finir, je vais juste revenir sur l'algorithme du tri à bulles d'hier:
- Dans le meilleurs cas (le tableau est déjà trié) il est en O(n)
- Dans le cas moyen il est en O(n²)
- Dans le pire des cas il est en O(n²)
Le fait que cet algorithme est en majorité du temps en O(n²) fait de lui un "mauvais" algorithme de tri. Nous verrons demain un autre algorithme de tri, théoriquement plus performant que le tri à bulles.
Voilà ! J'espère que ce billet un peu plus théorique que d'habitude vous a plu, rendez-vous demain pour la suite !